Here is the description
You are stranded in a casino (lucky you!) and need to purchase a flight home. Flights cost 250 dollars, but you have only 100 dollars at the moment. However, as I just said, you’re in a casino! Surely, you can gamble your way to 250 dollars.
The casino has a game called “Riddler’s Delight,” in which you can bet any amount of money in your possession for an even greater amount of money. You can even bet fractional (i.e., you can bet fractions of a penny), irrational or infinitesimal amounts if you so desire.
The catch is that the odds are not in your favor. In Riddler’s Delight, whenever you bet A dollars in an attempt to win B dollars (with B > A), your probability of winning is not A/B, which you would expect from a fair game. Instead, your probability of winning is always 10 percent less, or 0.9(A/B).
What should your betting strategy be to maximize your probability of getting home, and what is that probability?
The simplest thing to do is to just bet 100 dollars and hope to get 250 dollars in a single step. This strategy success with probability $0.9*100/250 = 0.36$. This is our baseline; a better strategy should improve on this probability.
First, it is important to realize that whatever you do, you want to always bet such that, if you win, you can walk out with 250. That’s because, after any bet, your expected position is worse-off than what you started with. Say you started with $A$ dollars and bet $a$ with the hopes of getting back $b$. The expected gain is
$$ E(A) = \left( 0.9\frac{a}{b} \right)(b - a) + \left( 1- 0.9\frac{a}{b} \right)(0 - a) = -0.1a $$
There are games where betting less agressively now will set yourself for success later. This is not one of them. Your position gets progressively worse over time. So you just want to maximize the odds of winning big just once.
Second, it is always better to bet in small numbers. Suppose that you bet $a$ with hopes of winning $250$. Your probability of succeeding is $$P(\rm success) = 0.9 \frac{a}{250}$$ But if you had instead bet $a/2$ and $a/2$ in two separate bets, expecting to win $b-a/2$ and $b$ in the second round (so that you are left with $b$ if you win either rounds). $$P(\rm success, separate) = 1-P(\rm fail) = 1- \left(1-0.9 \frac{a/2}{250-a/2}\right)\left(1-0.9 \frac{a/2}{250}\right)$$ You can check that $P(\rm success, separate) > P(\rm success)$.
For any bet, it then makes sense to divide the bet into smaller amounts. You can actually keep doing this till each bet become infinitesimally small. The probability of succcess in this case is,
$$ \begin{align*} P(\text{ success, infinitesimal bet}) &= 1-P(\rm fail, infinitesimal ) \newline &= 1- \lim_{\epsilon \to 0}\prod_{j=1}^{100/\epsilon} \left(1-0.9\frac{\epsilon}{250 - (100 - j\epsilon)} \right) \end{align*}$$
We can evaluate this to $0.368554$.
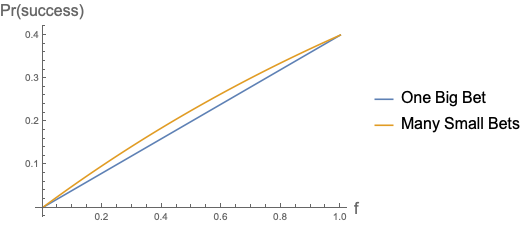
One might wonder: What if the “bias” against winning probability wasn’t 0.9 but some other fraction $f$? That plot is below. It seems that the “betting infinitesimally small bets” is always better than making one big bet. And, the advantage is largest for bias about 0.5.