This post is a response to Zach Wissner-Gross’s August 5th Riddler puzzle
Riddler Classic
Here is the problem description.
Magritte the bowler is back! This time, he is competing head-to-head against fellow bowler Fosse. However, rather than knocking down 10 pins arranged in a triangular formation, they are trying to knock down $N^2$ pins (where $N$ is some very, very large number) arranged in a rhombus, as shown below:
When Magritte rolls, he always knocks down the topmost pin. Then, if any pin gets knocked down, it has a 50 percent chance of knocking down either of the two pins directly behind it, independently of each other. (If there is only one pin directly behind it, then it too has a 50 percent chance of being knocked over.)
Fosse is a stronger bowler than Magritte. Like Magritte, she always knocks down the topmost pin. But each pin that’s knocked down then has a 70 percent chance (rather than Magritte’s 50 percent) of knocking down any of the pins directly behind it.
What are Magritte’s and Fosse’s respective probabilities of knocking down the bottommost pin in the rhombus formation?
I tried deriving a recursive relation between probabilities of pins being knocked out layer by layer. This approach wasn’t very fruitful. The solutions I was getting would take too long to compute.
It took me a while to realize that you can reduce this problem to that of finding a directed path in a random-bond square lattice.
In a square lattice with $N^2$ vertices, we randomly sample edges. Any two nearest neighboring vertices are connected with probability $p$. In terms of bowling pins, two vertices (or pins) are connected if knocking the first pin knocks the second pin too. The last pin gets knocked if there is exists a continguous and directed path (since we cannot travel back in time) between the first pin and the last.
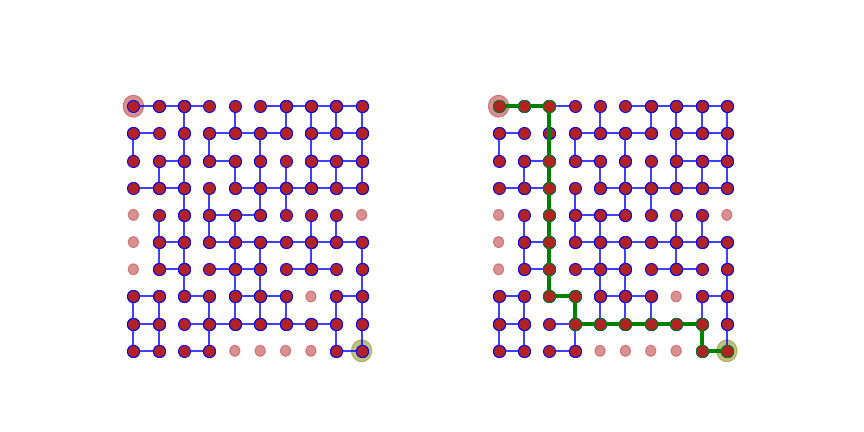
This sounds like something that should be probably is well-studied. Corner-to-corner percolation in (1+1D) square lattices? But I don’t know of any results on top of my head.
To get to my estimate of the result, I sampled 1000 instances of bond condiguration in 2D square lattices and then used a DFS search algorithm to see if there is a connected path from the top-left corner to the bottom-right corner.
The probability of percolation (or the last pin being knocked) looks like the following:
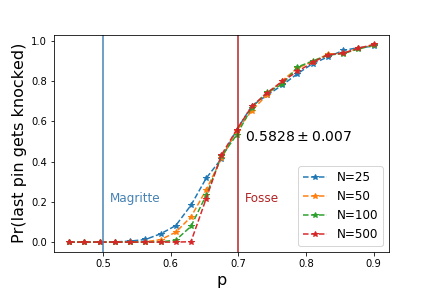
I expected there to be a threshold below which the probability is 0. However, I had also expected the probability to immediately jump to $1$ for all $p$ above the threshold.
I estimate this to be $0.5828 \pm 0.007$